Cálculo de redes de distribución de aire (II)

octubre 9, 2016

Cálculo de carga térmica de calefacción de una vivienda

octubre 25, 2016

Cálculo de redes de distribución de aire (III)

¡Hola a todos! Aquí traemos el último artículo de la serie de redes de distribución de aire, esta vez calculando la red de conductos mediante el método de reducción de velocidad, que permite un diseño de la red bastante adecuado, y es el más sencillo de emplear cuando no disponemos de software informático. Finalmente, haremos un breve estudio comparativo entre los tres métodos de cálculo, reducción de velocidad, pérdida de carga constante y recuperación estática, contrastando sus ventajas e inconvenientes en cuanto a coste de material e instalación, y costes de explotación derivados del consumo energético. Espero que sea de vuestro interés.

ÍNDICE

CÁLCULO DE CONDUCTOS POR EL MÉTODO DE REDUCCIÓN DE VELOCIDAD

Este método de cálculo consiste en fijar velocidades máximas en cada tramo de conducto, de manera que esta sea mayor en el conducto principal y vaya disminuyendo en las derivaciones para evitar ruidos excesivos en las zonas ocupadas. En la Tabla 1 se muestran las velocidades máximas recomendadas en conductos principales y derivaciones para diferentes tipos de establecimientos.

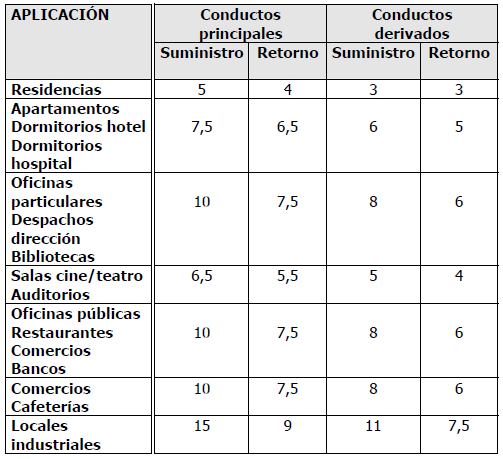
tabla1

Tabla 1. Velocidades máximas, en m/s, recomendadas en conductos de distribución de aire.

Recopilamos brevemente la información relevante tratada ya en los anteriores artículos:

Diámetro equivalente:

(1) $\begin{equation*} D_{eq}=1,3\cdot \frac{(H \cdot W)^{0,625}}{(H+W)^{0,25}}$ \end{equation*}$

Siendo:

$H,$ la altura del conducto

$W,$ la anchura del conducto

Pérdidas de carga unitarias (mm.c.a/m) (Figura 1):

(2) $\begin{equation*} h_f=2,09 \cdot 10^{-3} \cdot \frac{\dot{V}^{1,82}}{{D_{eq}}^{4,86}}$ \end{equation*}$

Siendo:

$\dot{V},$ el caudal de aire (m³/s)

$D_{eq},$ el diámetro equivalente (m)

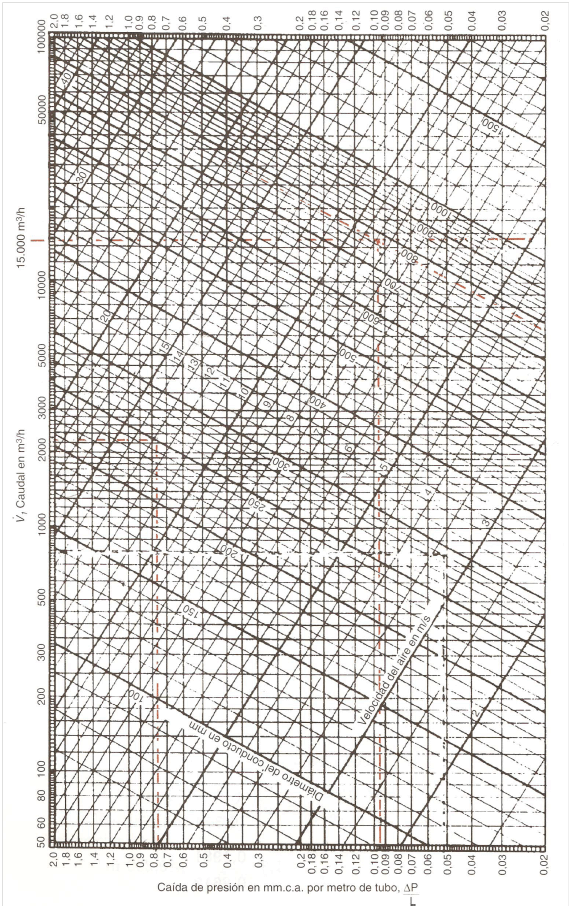
Figura 1. Gráfico para el cálculo de la pérdida de carga en conductos de fibra de vidrio.

Longitud equivalente (m): $L_{eq},$ Longitud modificada del conducto, que incluye también las singularidades (codos, curvas y accesorios). Suele tomarse habitualmente como la longitud de tramo recto de conducto mayorada en un 50 %, es decir, $L_{eq}=1,5L$

Recuperación estática (mm.c.a):

(3) $\begin{equation*} H_r=0,75\cdot \frac{v_{1}^{2}-v_{2}^{2}}{16}$ \end{equation*}$

Siendo:

$v_{1},$ la velocidad antes de la descarga de aire (m/s)

$v_{2},$ la velocidad después de la descarga de aire (m/s)

Caudal vs Sección:

(4) $\begin{equation*} \dot{V}=v \cdot S$ \end{equation*}$

Siendo:

$\dot{V},$ el caudal volumétrico de aire (m³/s)

$v,$ la velocidad del aire (m/s)

$S,$ la sección útil del conducto (m²)

CÁLCULO DE LA RED

En la Figura 2 podemos ver el esquema de la red.

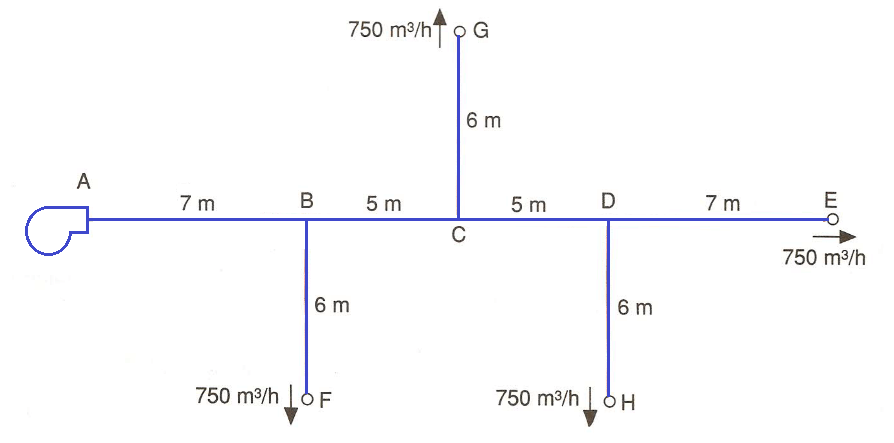
figura2

Figura 2. Esquema de la red de distribución de aire.

Longitudes y caudales de cada tramo (Tabla 2):

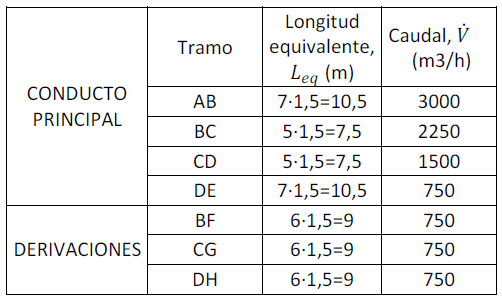
tabla1

Tabla 2. Longitudes equivalentes y caudales de cada tramo.

CONDUCTO PRINCIPAL

– Tramo AB

Procedemos limitando la velocidad del conducto, por ejemplo en 7,5 m/s, velocidad adecuada para conductos principales de impulsión en hoteles y apartamentos según la Tabla 1:

$S_{AB}=\dfrac{\dot{V}_{AB}}{v_{AB}}=\dfrac{0,8333}{7,5}=0,111m^2$

Conducto de 600×200 mm → S_AB=0,12 m² → v_AB=6,94 m/s → D_eqAB = 365 mm → h_fAB = 0,2 mm.c.a/m

– Tramo BC

Seguimos limitando la velocidad a 7,5 m/s, puesto que seguimos aún en el conducto principal:

$S_{BC}=\dfrac{\dot{V}_{BC}}{v_{BC}}=\dfrac{0,625}{7,5}=0,0833m^2$

Conducto de 450×200 mm → S_BC=0,09 m² → v_BC=6,94 m/s → D_eqBC = 321 mm → h_fBC = 0,221 mm.c.a/m

Recuperación estática en Tramo BC:

$H_{rBC}=0,75 \cdot \dfrac{6,94^2-6,94^2}{16}=0mm.c.a$

– Tramo CD

Velocidad = 7,5 m/s:

$S_{CD}=\dfrac{\dot{V}_{CD}}{v_{CD}}=\dfrac{0,417}{7,5}=0,0555m^2$

Conducto de 300×200 mm → S_CD=0,06 m² → v_CD=6,94 m/s → D_eqCD = 266 mm → h_fCD = 0,263 mm.c.a/m

Recuperación estática en Tramo CD:

$H_{rCD}=0,75 \cdot \dfrac{6,94^2-6,94^2}{16}=0mm.c.a$

– Tramo DE

Puesto que ya llegamos a una rejilla, consideraremos este tramo ya como una derivación, a efectos de velocidad, y limitaremos la velocidad a 6 m/s, tal como se indica en la Tabla 1:

$S_{DE}=\dfrac{\dot{V}_{DE}}{v_{DE}}=\dfrac{0,208}{6}=0,0347m^2$

Conducto de 200×200 mm → S_DE=0,04 m² → v_DE=5,21m/s → D_eqDE = 219 mm → h_fDE = 0,195 mm.c.a/m

Recuperación estática en Tramo DE:

$H_{rDE}=0,75 \cdot \dfrac{6,94^2-5,21^2}{16}=0,986mm.c.a$

Una vez calculados todos los tramos del conducto principal, recopilemos los datos obtenidos en la Tabla 3:

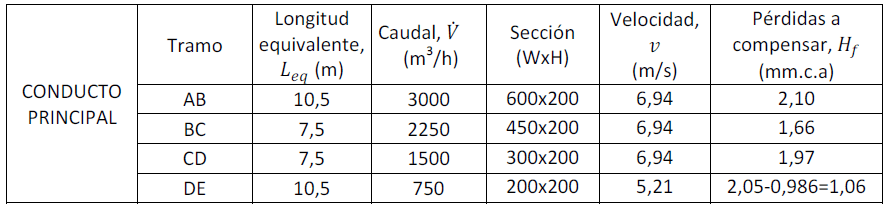
Tabla 3. Resultados de cálculo del conducto principal.

Seleccionamos rejilla de 425×225 mm, con caudal de 750 m3/h y una pérdida de carga de 2,6 mm.c.a

Presión necesaria en cabeza del conducto principal (Punto A):

$H_{A}=\sum{H_{f}}=2,10+1,66+1,97+1,06+2,6=9,39mm.c.a$

Por tanto, el ventilador que seleccionemos deberá de proporcionar un caudal de 3000 m3/h y una presión de 9,39 mm.c.a.

Queda definido el conducto principal y el ventilador. Vamos ahora a calcular las derivaciones:

DERIVACIONES

Puesto que en todas las derivaciones el caudal es igual al de la boca de impulsión del Punto E (750 m³/h), seleccionaremos las mismas rejillas que en dicho punto. Esto es, rejillas de 425×225 mm, con pérdida de carga 2,6 mm.c.a.

– Tramo BF

Puesto que estamos en una derivación, limitaremos la velocidad a 6 m/s, tal como se indica en la Tabla 1:

$S_{BF}=\dfrac{\dot{V}_{BF}}{v_{BF}}=\dfrac{0,208}{6}=0,0347m^2$

Conducto de 200×200 mm → S_BF=0,04 m² → v_BF=5,21m/s → D_eqBF = 219 mm → h_fBF = 0,195 mm.c.a/m

Recuperación estática en Tramo BF:

$H_{rBF}=0,75 \cdot \dfrac{6,94^2-5,21^2}{16}=0,986mm.c.a$

Equilibrado del ramal:

La única rejilla que está equilibrada de manera natural es la del Punto E, final del conducto principal. El resto de rejillas tendrán más presión de la necesaria, por lo que debemos regularlas para crear una pérdida de carga adicional, reduciendo así el caudal para que quede ajustado al de proyecto, y que la rejilla más desfavorable (Punto E) pueda tener también su caudal de proyecto.

Para saber cuanto hay que regular la rejilla del Punto F, tenemos que ver la diferencia entre la presión disponible en cabeza del ramal (Punto B) y la caída de presión en el ramal:

$H_{equil-F}=H_{B}-H_{fBF}$

Necesitamos conocer la presión en el Punto B, la cual será igual a la presión en el Punto A menos la pérdida de carga del Tramo AB. Y además le sumaremos la recuperación estática por la caída de velocidad hacia el ramal:

$H_{B}=H_{A}-H_{fAB}+H_{rBF}=9,39-2,10+0,986=8,28mm.c.a$

Por otra parte, la pérdida de carga en el ramal BF será igual a la pérdida de carga en el conducto más la pérdida de carga en la rejilla F:

$H_{fBF}=h_{fBF} \cdot L_{eqBF} + H_{f-rejillaF}=9 \cdot 0,195 + 2,6 = 4,35 mm.c.a$

Y ya podemos calcular el exceso de presión que habrá que equilibrar ajustando la compuerta de la rejilla F:

$H_{equil-F}=H_{B}-H_{fBF}=8,28-4,35=3,93mm.c.a$

Este ajuste se puede hacer con un medidor de caudal o un anemómetro, conocida la sección de paso de la rejilla.

– Tramo CG

Procediendo de manera similar al ramal anterior, dimensionamos el conducto:

$S_{CG}=\dfrac{\dot{V}_{CG}}{v_{CG}}=\dfrac{0,208}{6}=0,0347m^2$

Conducto de 200×200 mm → S_CG=0,04 m² → v_CG=5,21m/s → D_eqCG = 219 mm → h_fCG = 0,195 mm.c.a/m

Recuperación estática en Tramo CG:

$H_{rCG}=0,75 \cdot \dfrac{6,94^2-5,21^2}{16}=0,986mm.c.a$

Equilibrado del ramal:

$H_{equil-G}=H_{C}-H_{fCG}$

$H_{C}=H_{B}-H_{fBC}+H_{rCG}=7,29-1,66+0,986=6,62mm.c.a$

$H_{fCG}=h_{fCG} \cdot L_{eqCG} + H_{f-rejillaG}=9 \cdot 0,195 + 2,6 = 4,35 mm.c.a$

Y el exceso de presión que habrá que equilibrar ajustando la compuerta de la rejilla G será:

$H_{equil-G}=H_{C}-H_{fCG}=6,62-4,35=2,27mm.c.a$

– Tramo DH

Procediendo de nuevo como en los demás ramales:

$S_{DH}=\dfrac{\dot{V}_{DH}}{v_{DH}}=\dfrac{0,208}{6}=0,0347m^2$

Conducto de 200×200 mm → S_DH=0,04 m² → v_DH=5,21m/s → D_eqDH = 219 mm → h_fDH = 0,195 mm.c.a/m

Recuperación estática en Tramo DH:

$H_{rDH}=0,75 \cdot \dfrac{6,94^2-5,21^2}{16}=0,986mm.c.a$

Equilibrado del ramal:

$H_{equil-H}=H_{D}-H_{fDH}$

$H_{D}=H_{C}-H_{fCD}+H_{rDH}=5,63-1,97+0,986=4,65mm.c.a$

$H_{fDH}=h_{fDH} \cdot L_{eqDH} + H_{f-rejillaH}=9 \cdot 0,195 + 2,6 = 4,35 mm.c.a$

Y el exceso de presión que habrá que equilibrar ajustando la compuerta de la rejilla H será:

$H_{equil-H}=H_{D}-H_{fDH}=4,65-4,35=0,3mm.c.a$

Ya podemos recopilar toda la información del cálculo de la red en una tabla resumen:

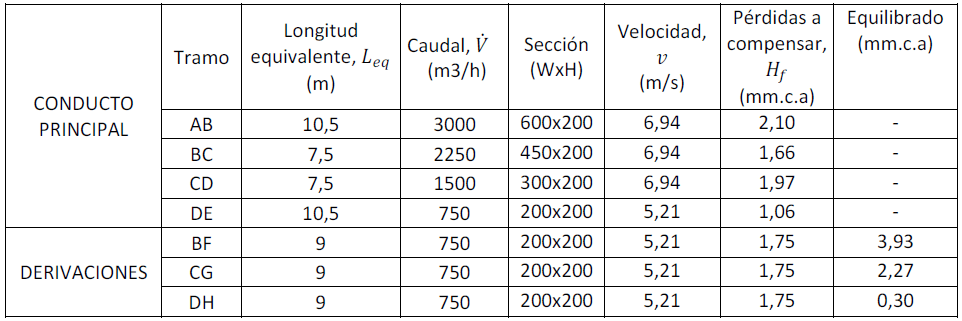
Tabla 4. Resumen del cálculo de la red por el método de reducción de velocidad.

COMPARACIÓN DE LOS TRES MÉTODOS PARA EL CÁLCULO DE CONDUCTOS

Vamos ahora a ver los costes de los conductos y el equipo de ventilación para cada caso:

Precio panel fibra vidrio: 16 €/m²
Precio caja ventilación para Métodos 1 y 3: Caja 10/10- 3/4 CV: 989 €
Precio caja ventilación para Método 2: Caja 10/10- 1/2 CV: 969 €

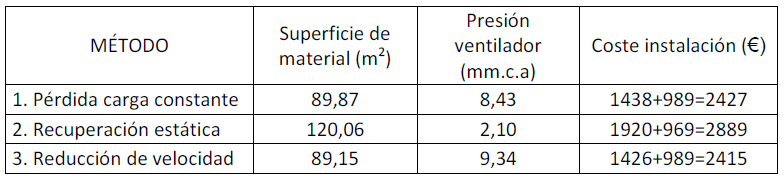
tabla4

Tabla 5. Comparación de los costes de instalación con los diferentes métodos de cálculo.

Podemos ver que el coste de instalación más bajo es el del Método 3: Reducción de velocidad, con el cual se ahorra más material. El Método 2: Pérdida de carga constante, tiene unos costes de instalación muy similares también. Sin embargo, el Método 2: Recuperación estática, presenta unos costes mayores, debido al mayor tamaño de los conductos. Para los tres casos los costes de los equipos de ventilación son muy similares, ya que aunque con el Método de recuperación estática necesitamos menos presión en la red, las cajas de ventilación comerciales tienen unos tamaños estandarizados, lo que lleva a un equipo sobredimensionado en muchos casos.

No obstante, si se trata de una instalación con una red de gran tamaño y donde, además, podemos adaptar la potencia del ventilador a la demanda de la red mediante variador de velocidad, el Método de recuperación estática puede presentar gran ahorro en el consumo eléctrico que podría compensar el sobrecoste de la instalación inicial.

Por ejemplo, para el caso que nos ocupa, vamos a comparar los costes de explotación para los tres métodos, considerando por ejemplo, que la instalación de ventilación funciona 18 horas al día durante 20 años, y que ajustaremos en todo momento la potencia del ventilador a las condiciones de presión y caudal requeridas por la red de conductos. Tomaremos el precio de la energía como 0,1 €/kWh. Los resultados se muestran en la Tabla 6, donde podemos ver que con el Método de recuperación estática se obtienen ahorros de más de un 75 % en el consumo eléctrico.

Tabla 5. Comparación de los costes de explotación con los diferentes métodos de cálculo.

Si comparamos de manera simultánea los costes de instalación y explotación, obtenemos los siguientes resultados globales (Tabla 6):

Tabla 6. Comparación de los costes globales con los diferentes métodos de cálculo.

Vemos como comparando los costes globales de instalación y explotación, los tres métodos se asemejan bastante, aunque el Método de recuperación estática tendría un coste global más bajo a lo largo de la vida útil de la instalación. No obstante, si la vida útil fuera inferior a la fijada en el ejemplo, el ahorro de material tendrá más peso que el consumo energético. Para obtener un método de diseño optimizado, podríamos programar un software informático que calculara la red de conductos teniendo en cuenta los costes de instalación (material y equipos ) y explotación (consumo de energía), y minimizara el coste global. Existen softwares que permiten el diseño y cálculo de la red por diferentes métodos, como el software gratuito DUCTO de ATECYR, algunos otros más sencillos como el de los fabricantes de conductos URSA o ISOVER.

Pues aquí termina esta serie de artículos, aunque si hay sugerencias o dudas sobre el tema de las redes de conductos, podemos preparar un nuevo artículo ampliando información o tratando alguna consulta e concreto. Espero vuestros comentarios. ¡Buena semana a todos!

¿Te gustó este artículo? ¡Compártelo!