¡Buenas tardes frigoristas! Vamos hoy con la segunda parte del artículo Enfriamiento de líquidos: Selección de equipos y tiempos de enfriamiento, cuya primera parte publicamos la pasada semana. ¡Espero que sea de interés!
Enfriamiento de líquidos: Selección del equipo y tiempos de enfriamiento (I)
septiembre 11, 2016
Vasos de expansión: Utilidad y mantenimiento
septiembre 20, 20164. SISTEMA 3: ENFRIAMIENTO DE UN LÍQUIDO CON UN TANQUE Y UN INTERCAMBIADOR DE CALOR EXTERNO
Este método consiste en recircular el agua haciéndola pasar por un intercambiador externo y devolviéndola al tanque tras ser enfriada. Es quizás el problema más complejo de analizar de los vistos hasta ahora, ya que la temperatura del agua del tanque va disminuyendo progresivamente, y por tanto, la temperatura del agua que entra en el intercambiador de calor es variable, así como la temperatura de salida. Esto hace que, al igual que en el Sistema 2, el salto térmico entre el agua y el refrigerante sea variable (Figura 7).
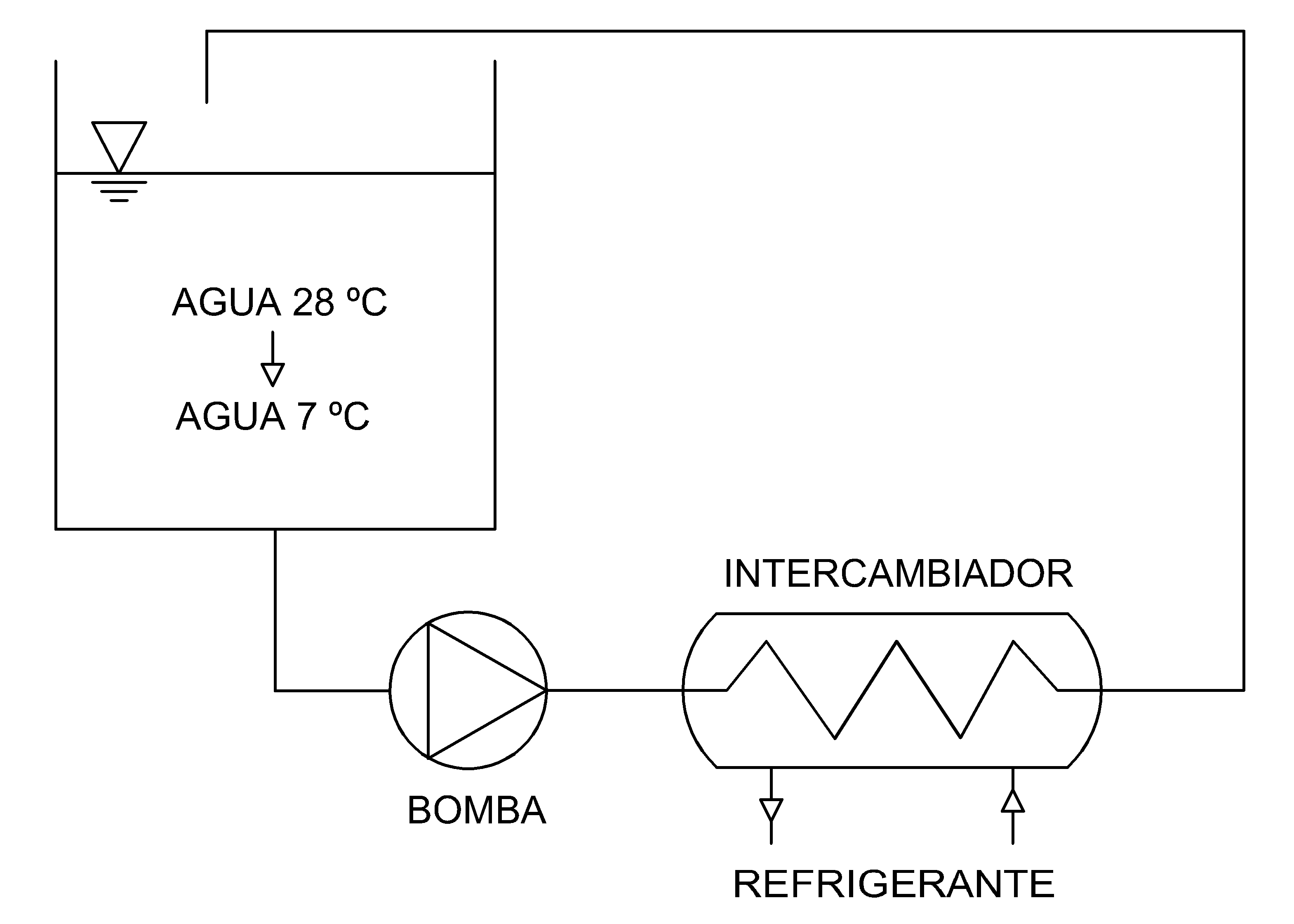Figura 7. Esquema de enfriamiento mediante un tanque y un intercambiador de calor externo.
Las ecuaciones matemáticas que gobiernan este proceso son bastante complejas, y si alguien está interesado, puedo dedicar una entrada a este tema. No obstante, el resultado del análisis matemático permite obtener una fórmula bastante similar a la Ley de enfriamiento de Newton que vimos anteriormente, siendo la única diferencia en este caso que el coeficiente de transmisión de calor, K, va a ser sustituido por otro coeficiente, Γ, que depende de los caudales másicos de refrigerante y agua, además del propio coeficiente de transmisión del intercambiador, K (Ecuación 1).
(1) 
Siendo:
el tiempo de enfriamiento, en segundos
la densidad del agua = 1000 kg/m3
el calor específico del agua = 4186 J/kg ºC
el volumen de agua = 1 m3
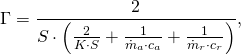coeficiente corregido donde:
es el coeficiente global de transmisión de calor del intercambiador = 3320 W/m2K (consideraremos que empleamos como refrigerante propilenglicol + agua, en condiciones similares al Sistema 1 visto anteriormente. Os invito a probar con refrigerante R-134a para obtener otra variante).
Tenemos una serie de variables, desconocidas en principio, con las que podemos jugar en el software de cálculo del intercambiador para obtener el punto más favorable en equilibrio con la Ecuación 1 para el tiempo. Estas variables son:
el caudal de agua (1000L en 1 hora) = ¿?
el caudal de refrigerante = ¿?
el calor específico del refrigerante = 3560 J/kg ºC (propilenglicol)
la superficie de intercambio = ¿?
la temperatura de entrada del refrigerante = ¿?
Para comenzar a aproximarnos a la solución óptima, tomaremos un valor de Tre = 6 ºC, ya que es el más alto posible para poder enfriar a contracorriente agua hasta 7 ºC, y que ya empleamos en el Sistema 1. Tras tomar ese valor, usamos la Ecuación 1 y el software de simulación de SWEP, y comprobamos que el salto térmico entre el refrigerante y el agua es insuficiente, ya que, a diferencia del Sistema 1, en este caso el agua que va entrando al intercambiador está cada vez más fría, y esto hace que el tiempo de enfriamiento se alargue más de lo previsto. La única manera de poder usar refrigerante a 6 ºC sería aumentando enormemente los caudales de los fluidos en el intercambiador, así como la superficie del mismo, provocando un sobrecoste de bombeo e instalación. Por otra parte, podríamos dejar los caudales y la superficie de intercambio al mínimo, y bajar mucho la temperatura del refrigerante, pero eso supondría un gasto energético excesivo.
Nuestro objetivo final es conseguir enfriar el tanque en 1 hora. Tras varias iteraciones aproximativas, jugando con los caudales de refrigerante y agua, así como con la superficie del intercambiador y la temperatura del refrigerante, se puede llegar a una solución de equilibrio en cuanto a volumen de la instalación y gasto energético de la misma:
Potencia térmica intercambiada = 35,11 kW
Temperatura inicial del tanque = 28 ºC
Temperatura final del tanque =7 ºC
Temperatura del refrigerante a la entrada = 2 ºC
Caudal de agua = 0,4 kg/s
Caudal de refrigerante = 1,77 kg/s
Superficie de intercambio = 1,96 m2
Conocidos estos resultados, es el momento de comparar los tres sistemas de enfriamiento analizados y ver las ventajas e inconvenientes de cada uno de ellos.
5. ESTUDIO COMPARATIVO DE LOS DIFERENTES SISTEMAS DE ENFRIAMIENTO DE LÍQUIDO
En la Tabla 1 se muestra de manera simplificada una comparativa de los tres sistemas. Para los tres casos se ha considerado que se emplea como refrigerante agua + propilenglicol al 20 %.Podemos ver que el Sistema 1 es el que tiene un mejor rendimiento energético desde el punto de vista frigorífico, y esto contribuye a menores gastos de explotación, aunque requiere de grupo de bombeo para agua y glicol. Por otra parte, se precisa de una costosa inversión inicial debido a que se emplean dos tanques de almacenamiento.
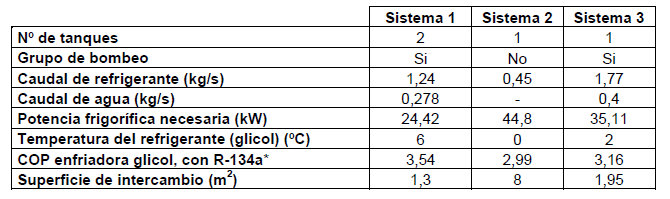
Tabla 1. Comparativa de los tres sistemas de enfriamiento de líquidos (*Equipo de R-134a trabajando con Temperatura condensación 45 ºC, Recalentamiento y Subenfriamiento de 5 K).
El Sistema 2 es sin duda el más económico en cuanto a instalación inicial, sin necesidad de grupo de bombeo de agua, pero requiere un equipo frigorífico trabajando con un COP más bajo. Además, el coste debido a la superficie de intercambio es muy elevado en comparación con los demás sistemas. Esto es consecuencia del bajo coeficiente de transmisión, K, del serpentín sumergido. En cualquier caso, es un sistema muy empleado cuando el fluido a enfriar es de tipo alimentario (marmitas de caldo), y las labores de limpieza hacen difícil emplear intercambiadores de calor externos al depósito.
Por último, vemos que el Sistema 3, con recirculación del líquido a través de un intercambiador externo, es el más equilibrado en cuanto al coste de instalación y el consumo energético de los equipos, situándose en valores intermedios entre los dos sistemas anteriores. Este método de enfriamiento es muy empleado para enfriar rápidamente fluidos de proceso industrial, sobre todo si dicho fluido no presenta muchas impurezas que puedan obstruir el intercambiador de calor.
Aquí termina esta segunda parte sobre la selección del sistema de enfriamiento de líquidos. Espero que haya sido de utilidad y que abra las puertas a futuros debates de interés. Como siempre, cualquier comentario será bienvenido. Un saludo a todos y ¡buen comienzo de semana!
¿Te gustó este artículo? ¡Compártelo!
2 Comments
Muchas gracias por la explicación, no tengo apenas idea sobre la materia pero esto me ayudará con mis cálculos.
Te planteo mis dudas para que me deis vuestra opinión por favor. Tengo un equipo electrico de 10kw y quiero utilizar un sistema de enfriamiento por inmersión con un líquido dieléctrico especial para este tipo de sistemas.
El líquido pasará por un intercambiador de calor que utilizará como refrigerante agua. Las especificaciones del sistema de enfriamiento que quiero adquirir indican que se necesita un caudal de 0.3m3/h de agua a 20°C para poder refrigerar dicho equipo. Desconozco a esa potencia a que temperatura saldrá el agua del intercambiador de calor, pero necesitaba saber que método me recomendáis para enfriar el agua. La presión sonora/nivel de ruido es determinante en este caso, ya que se trata de una instalación casera para pruebas de laboratorio de procesamiento de datos (el sistema funcionará 24×7). Muchas gracias.
Hola gbarcia,
Necesitaría algunos detalles más para poder ayudarte y un pequeño esquema del sistema que pretendes instalar. Envíame un email a fjenriquez@coolproyect.es y lo comentamos.
Un saludo.