Salto térmico y humedad en la cámara frigorífica

septiembre 25, 2016

Cálculo de redes de distribución de aire (II)

octubre 9, 2016

Cálculo de redes de distribución de aire (I)

¡Buenas tardes compañeros! Hoy vamos a comenzar una serie de artículos dedicados a las redes de distribución de aire. Existe mucha confusión respecto a cómo se calculan las redes de conductos para climatización y ventilación, sobre todo debido a los diferentes métodos que existen para el cálculo, y que pocos libros y manuales tratan en profundidad. Por ello vamos a definir una red sencilla y vamos a calcular la sección de los conductos y las características del ventilador por los tres métodos más conocidos:

Método de pérdida de carga constante.
Método de recuperación estática.
Método de reducción de velocidad.

Realizado el cálculo por estos tres métodos, haremos un breve estudio económico para ver cual de ellos permite un mayor ahorro, tanto en instalación como en consumo de energía.

En este primer post, vamos a realizar el cálculo por el método de pérdida de carga constante. Espero que sea de vuestro interés.

CÁLCULO DE CONDUCTOS POR EL MÉTODO DE PÉRDIDA DE CARGA CONSTANTE

Este método es empleado desde hace mucho tiempo por los proyectistas de redes de distribución de aire, y consiste en diseñar la red de conductos de tal forma que la pérdida de carga lineal (mm.c.a/m), en cada ramal de la red, sea la misma.

Antes de plantear el problema en cuestión puede ser conveniente refrescar algunos conceptos básicos sobre circulación de aire en redes de conductos:

Diámetro equivalente: Sirve para transformar un conducto de sección rectangular en otro de sección circular equivalente, que nos facilita el cálculo de la red. Se define diámetro equivalente a aquel con el que un conducto tiene la misma pérdida de carga por fricción del aire que el conducto de sección rectangular que estemos estudiando. Su fórmula es la siguiente:

(1) $\begin{equation*} D_{eq}=1,3\cdot \frac{(H \cdot W)^{0,625}}{(H+W)^{0,25}}$ \end{equation*}$

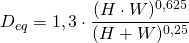
Siendo:

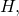$H,$ la altura del conducto

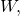$W,$ la anchura del conducto

Pérdidas de carga unitarias (mm.c.a/m): Son las pérdidas de presión por metro lineal debidas a la fricción entre el aire y las paredes de los conductos. Dependen del material del conducto, y para fibra de vidrio, pueden calcularse gráficamente (Figura 1) o mediante la siguiente fórmula:

(2) $\begin{equation*} h_f=2,09 \cdot 10^{-3} \cdot \frac{\dot{V}^{1,82}}{{D_{eq}}^{4,86}}$ \end{equation*}$

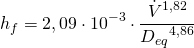
Siendo:

$\dot{V},$ el caudal de aire (m³/s)

$D_{eq},$ el diámetro equivalente (m)

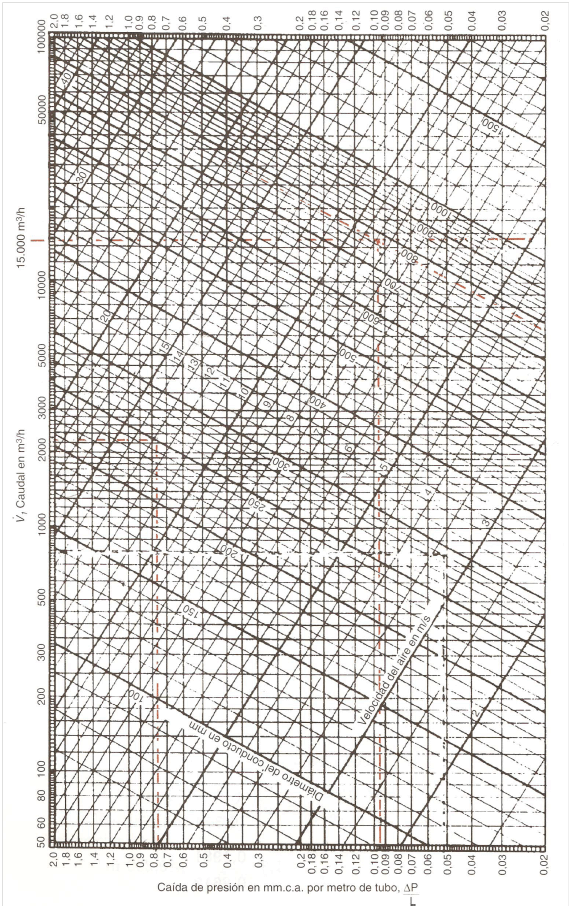
Figura 1. Gráfico para el cálculo de la pérdida de carga en conductos de fibra de vidrio.

Longitud equivalente (m): $L_{eq},$ Longitud modificada del conducto, que incluye también las singularidades (codos, curvas y accesorios). Suele tomarse habitualmente como la longitud de tramo recto de conducto mayorada en un 50 %, es decir, $L_{eq}=1,5L$

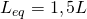
Recuperación estática (mm.c.a): Es la presión estática que se recupera en el conducto principal después de cada descarga a un ramal, debido a la caída de velocidad. Se calcula con la siguiente fórmula:

(3) $\begin{equation*} H_r=0,75\cdot \frac{v_{1}^{2}-v_{2}^{2}}{16}$ \end{equation*}$

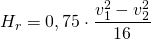
Siendo:

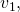$v_{1},$ la velocidad antes de la descarga de aire (m/s)

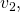$v_{2},$ la velocidad después de la descarga de aire (m/s)

Caudal vs Sección: Para un conducto de aire, conocido el caudal y la velocidad del aire, se puede calcular la sección de conducto a partir de la ecuación de continuidad:

(4) $\begin{equation*} \dot{V}=v \cdot S$ \end{equation*}$

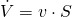
Siendo:

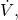$\dot{V},$ el caudal volumétrico de aire (m³/s)

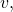$v,$ la velocidad del aire (m/s)

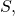$S,$ la sección útil del conducto (m²)

CÁLCULO DE LA RED

En la Figura 2 podemos ver el esquema de la red de distribución que vamos a analizar.

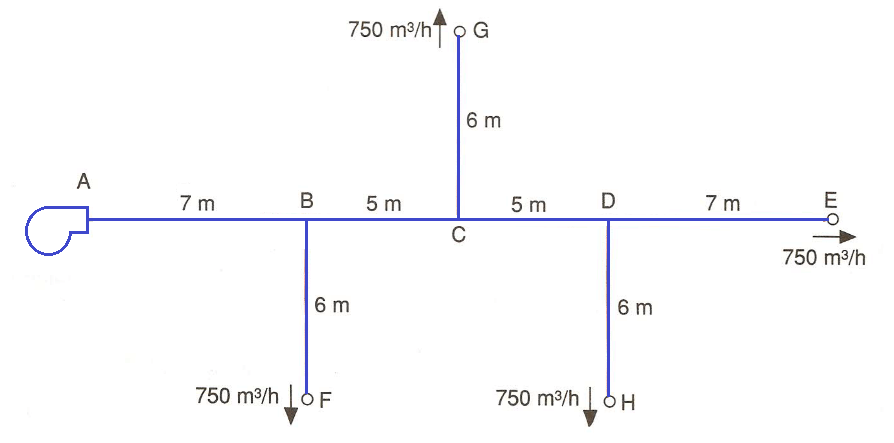
figura2

Figura 2. Esquema de la red de distribución de aire.

En primer lugar vamos a establecer las longitudes y caudales de cada tramo (Tabla 1). Como hemos comentado, mayoraremos la longitud de cada tramo en un 50 % en concepto de pérdidas de carga en singularidades:

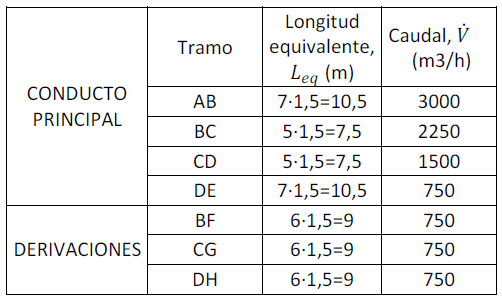
tabla1

Tabla 1. Longitudes equivalentes y caudales de cada tramo.

CONDUCTO PRINCIPAL

El conducto principal es, por definición, aquel que tiene una mayor pérdida de carga (habitualmente el de mayor longitud), de manera que dimensionando el ventilador para este conducto, tendremos también presión y caudal suficientes en los ramales secundarios. En redes de distribución complejas, a veces es difícil reconocer el conducto principal, y puede ser necesario hacer algunas comprobaciones previas. No obstante, para la red que vamos a analizar, se puede ver claramente que el conducto principal es el comprendido entre los Puntos A y E.

– Tramo AB

Puesto que conocemos el caudal que pasa por el Tramo AB, si fijamos la velocidad del aire, podremos obtener la sección del tramo mediante la ecuación de continuidad (Ec. 4). Fijaremos por ejemplo la velocidad máxima en el conducto principal en 7,5 m/s para evitar ruidos excesivos:

$S_{AB}=\dfrac{\dot{V}_{AB}}{v_{AB}}=\dfrac{0,8333}{7,5}=0,111m^2$

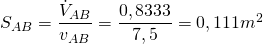
Vamos a seleccionar un conducto rectangular que tenga una sección mínima de 0,111 m², por ejemplo 600×200 mm. Mantendremos una altura de conducto de 200 mm para toda la red, por adaptarse adecuadamente a la altura útil disponible en los falsos techos.

Si seleccionamos un conducto de 600×200, tendremos una sección de 0,12 m² y una velocidad de 6,94 m/s. Ahora hallamos el diámetro circular equivalente del conducto rectangular elegido aplicando la Ecuación 1, siendo el resultado D_eqAB = 365 mm.

Por último, conocido el diámetro equivalente y el caudal del tramo, podemos hallar la pérdida de carga unitaria empleando la gráfica de la Figura 1: h_fAB = 0,2 mm.c.a/m. Fijaremos esta pérdida de carga para todo el conducto principal, como establece el método de pérdida de carga constante.

– Tramo BC

Fijada la pérdida de carga unitaria en 0,2 mm.c.a/m, y puesto que conocemos el caudal del tramo, 2250 m³/h, podemos obtener el diámetro equivalente de la gráfica de la Figura 1: D_eqBC = 328 mm. Seleccionaremos un conducto rectangular con altura 200 mm y que tenga aproximadamente ese diámetro equivalente (para ello usamos la Ecuación 1). Por ejemplo tomamos 500×200 mm, con las siguientes características:

S_BC = 0,10 m²
v_BC = 6,25 m/s (obtenida empleando la Ecuación 4 para el caudal y la sección del conducto BC)
D_eqBC = 337 mm
h_fBC = 0,176 mm.c.a/m

Por otra parte, puesto que acabamos de realizar una descarga de aire a un ramal, tendremos una recuperación de presión estática en el conducto principal:

$H_{rBC}=0,75 \cdot \dfrac{6,94^2-6,25^2}{16}=0,427mm.c.a$

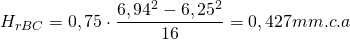
Esta recuperación de presión es un extra que se tiene en el Tramo BC debido a la descarga de aire que se realizó en el Punto B.

– Tramo CD

Procediendo de manera similar al Tramo BC, obtenemos los siguientes resultados:

D_eqCD = 282 mm → 350×200 mm → D_eqCD = 286 mm → h_fCD = 0,185 mm.c.a/m → v_CD = 5,95 m/s

Recordemos el proceso:

Selecciono de la gráfica de «caudal-pérdida de carga» un diámetro equivalente que cumpla con el caudal del tramo y con la pérdida de carga unitaria de 0,2 mm.c.a/m, la cual hemos fijado para toda la red.
Seleccionamos un conducto rectangular que se aproxime a ese diámetro equivalente.
Comprobamos el diámetro equivalente real de ese conducto que hemos seleccionado y obtenemos finalmente la pérdida de carga unitaria para ese conducto, la cual debería estar muy próxima a los 0,2 mm.c.a/m. También podemos hallar a velocidad del aire en el tramo mediante la Ecuación 4.

La recuperación estática en este tramo sería:

$H_{rCD}=0,75 \cdot \dfrac{6,25^2-5,95^2}{16}=0,172mm.c.a$

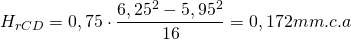
– Tramo DE

Procediendo igualmente de nuevo:

D_eqDE = 217 mm → 200×200 mm → D_eqDE = 219 mm → h_fDE = 0,195 mm.c.a/m → v_DE = 5,21 m/s

Recuperación estática en el tramo:

$H_{rDE}=0,75 \cdot \dfrac{5,95^2-5,21^2}{16}=0,387mm.c.a$

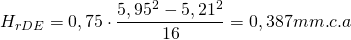
Una vez calculados todos los tramos del conducto principal, recopilemos los datos obtenidos en la Tabla 2:

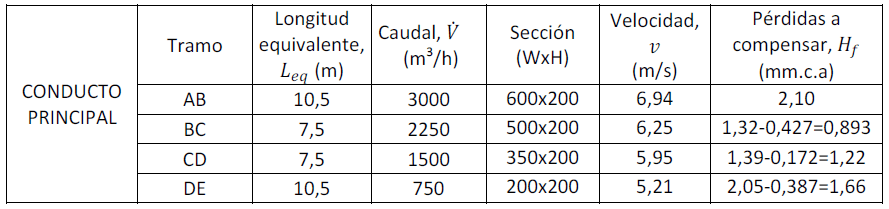
tabla2

Tabla 2. Resultados de cálculo del conducto principal.

En la columna «Pérdidas a compensar» vemos la pérdida de carga que se produce en cada tramo de conducto. Estas pérdidas se calculan multiplicando las pérdidas unitarias de cada tramo por su correspondiente longitud equivalente. Además, cada vez que haya una descarga de aire a un ramal, tendremos que restar la recuperación estática a la pérdida de carga del siguiente tramo.

Por otra parte, en el Punto E, tenemos una rejilla de impulsión. Es necesario seleccionar dicha rejilla para conocer la pérdida de carga adicional que provocará en el conducto principal. Miramos el catálogo de rejillas que se adjunta en el post, y seleccionamos una rejilla que produzca menos de 35 dB en las condiciones de trabajo (estipulado por el Reglamento de Instalaciones Térmicas, RITE, en España). Según esto, seleccionamos una rejilla 425×225 mm, que con caudal de 750 m3/h produce una pérdida de carga de unos 2,6 mm.c.a (Figura 3).

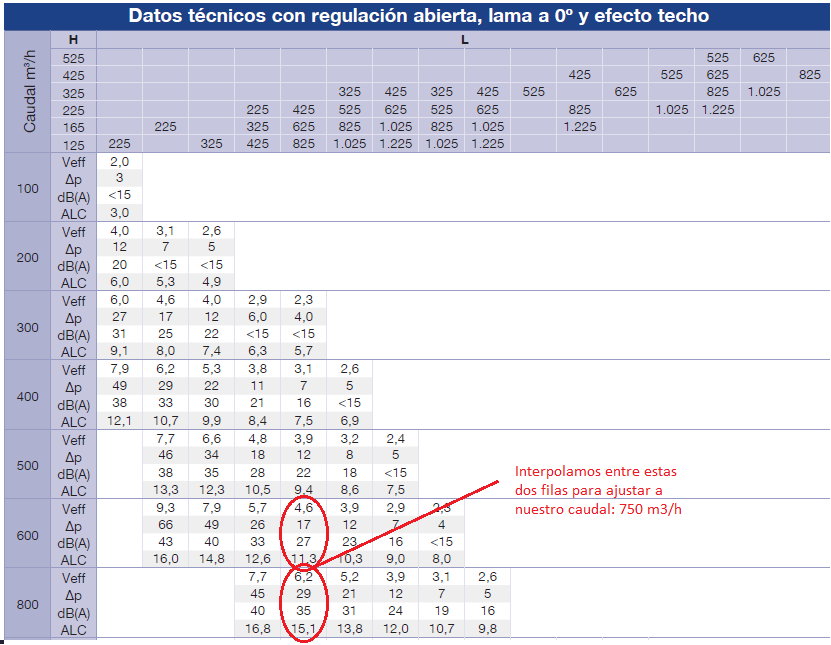
figura3

Figura 3. Selección de la rejilla.

Bien, pues ya estamos en disposición de calcular la presión necesaria en cabeza del conducto principal (Punto A), presión que deberá proporcionar el ventilador para que el aire llegue al punto más desfavorable (Punto E), y sea capaz de pasar por la rejilla hasta llegar al recinto a climatizar:

$H_{A}=\sum{H_{f}}=2,10+0,89+1,22+1,66+2,6=8,47mm.c.a$

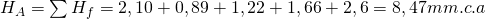
Por tanto, el ventilador que seleccionemos deberá de proporcionar un caudal de 3000 m3/h y una presión de 8,47 mm.c.a.

Queda definido el conducto principal y el ventilador. Vamos ahora a calcular las derivaciones:

DERIVACIONES

Puesto que en todas las derivaciones el caudal es igual al de la boca de impulsión del Punto E (750 m³/h), seleccionaremos las mismas rejillas que en dicho punto. Esto es, rejillas de 425×225 mm, con pérdida de carga 2,6 mm.c.a.

– Tramo BF

Puesto que hemos establecido una pérdida de carga constante de 0,2 mm.c.a/m para toda la red, seguiremos con este criterio también en los ramales. Así pues, si tomamos el caudal del tramo (750 m³/h) y vamos a la gráfica, podemos dimensionar el tramo al igual que hicimos con el conducto principal:

D_eqBF = 217 mm → 200×200 mm → D_eqBF = 219 mm → h_fBF = 0,195 mm.c.a/m → v_BF = 5,21 m/s

Recuperación estática en el tramo:

$H_{rBF}=0,75 \cdot \dfrac{6,94^2-5,21^2}{16}=0,985mm.c.a$

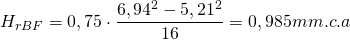
Equilibrado del ramal:

La única rejilla que está equilibrada de manera natural es la del Punto E, final del conducto principal. El resto de rejillas tendrán más presión de la necesaria, por lo que debemos regularlas para crear una pérdida de carga adicional, reduciendo así el caudal para que quede ajustado al de proyecto, y que la rejilla más desfavorable (Punto E) pueda tener también su caudal de proyecto.

Para saber cuanto hay que regular la rejilla del Punto F, tenemos que ver la diferencia entre la presión disponible en cabeza del ramal (Punto B) y la caída de presión en el ramal:

$H_{equil-F}=H_{B}-H_{fBF}$

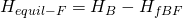
Necesitamos conocer la presión en el Punto B, la cual será igual a la presión en el Punto A menos la pérdida de carga del Tramo AB. Y además le sumaremos la recuperación estática por la caída de velocidad hacia el ramal:

$H_{B}=H_{A}-H_{fAB}+H_{rBF}=8,47-2,10+0,985=7,35mm.c.a$

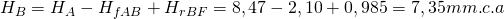
Por otra parte, la pérdida de carga en el ramal BF será igual a la pérdida de carga en el conducto más la pérdida de carga en la rejilla F:

$H_{fBF}=h_{fBF} \cdot L_{eqBF} + H_{f-rejillaF}=9 \cdot 0,195 + 2,6 = 4,35 mm.c.a$

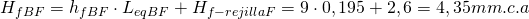
Y ya podemos calcular el exceso de presión que habrá que equilibrar ajustando la compuerta de la rejilla F:

$H_{equil-F}=H_{B}-H_{fBF}=7,35-4,35=3mm.c.a$

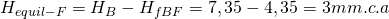
Este ajuste se puede hacer con un medidor de caudal o un anemómetro, conocida la sección de paso de la rejilla.

– Tramo CG

Procediendo de manera similar al ramal anterior, dimensionamos el conducto:

D_eqCG = 217 mm → 200×200 mm → D_eqCG = 219 mm → h_fCG = 0,195 mm.c.a/m → v_CG = 5,21 m/s

Recuperación estática en el tramo (ahora teniendo en cuenta la velocidad del aire que circulaba por el conducto principal antes de llegar al Punto C de derivación):

$H_{rCG}=0,75 \cdot \dfrac{6,25^2-5,21^2}{16}=0,559mm.c.a$

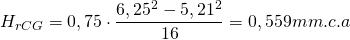
Equilibrado del ramal:

$H_{equil-G}=H_{C}-H_{fCG}$

$H_{C}=H_{B}-H_{fBC}+H_{rCG}=6,37-0,893+0,559=6,04mm.c.a$

$H_{fCG}=h_{fCG} \cdot L_{eqCG} + H_{f-rejillaG}=9 \cdot 0,195 + 2,6 = 4,35 mm.c.a$

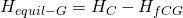
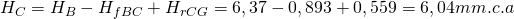
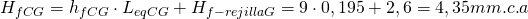
Y el exceso de presión que habrá que equilibrar ajustando la compuerta de la rejilla G será:

$H_{equil-G}=H_{C}-H_{fCG}=6,04-4,35=1,69mm.c.a$

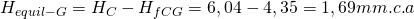
– Tramo DH

D_eqDH = 217 mm → 200×200 mm → D_eqDH = 219 mm → h_fDH = 0,195 mm.c.a/m → v_DH = 5,21 m/s

Recuperación estática en el tramo (ahora teniendo en cuenta la velocidad del aire que circulaba por el conducto principal antes de llegar al Punto D de derivación):

$H_{rDH}=0,75 \cdot \dfrac{5,95^2-5,21^2}{16}=0,387mm.c.a$

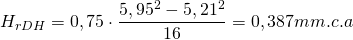
Equilibrado del ramal:

$H_{equil-H}=H_{D}-H_{fDH}$

$H_{D}=H_{C}-H_{fCD}+H_{rDH}=5,48-1,22+0,387=4,65mm.c.a$

$H_{fDH}=h_{fDH} \cdot L_{eqDH} + H_{f-rejillaH}=9 \cdot 0,195 + 2,6 = 4,35 mm.c.a$

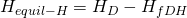
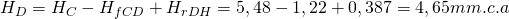
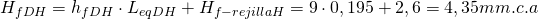
Y el exceso de presión que habrá que equilibrar ajustando la compuerta de la rejilla H será:

$H_{equil-H}=H_{D}-H_{fDH}=4,65-4,35=0,30mm.c.a$

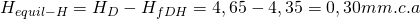
Ya podemos recopilar toda la información del cálculo de la red en una tabla resumen:

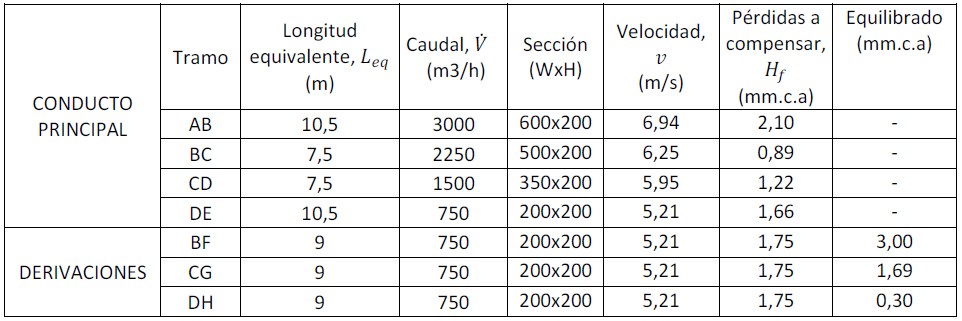
tabla3

Tabla 3. Resumen del cálculo de la red por el método de pérdida de carga constante.

Bueno compañeros, pues hasta aquí llega esta entrada. La semana que viene continuaremos con el método de recuperación estática. Espero que os sea de interés. Si hay cualquier duda, por favor, escribid en comentarios y estaré a vuestra disposición para resolverla. Puede parecer un cálculo engorroso, pero la mecánica es sencilla, y muy fácil de programar en una hoja de Excel. ¡Buena semana a todos!

¿Te gustó este artículo? ¡Compártelo!

Fran Enríquez

19 Comments

Jesus Bernal dice:
octubre 3, 2016 a las 8:01 am
Gracias. Esta vez más didáctico que otras, o tal vez me lo pareció a mí por ser tema más sencillo. Aprendí además un concepto nuevo que no me han enseñado a aplicar, la «recuperación estática». No lo había oído nunca y no la he tenido nunca en cuenta. Un saludo.
Accede para responder
- Fran Enríquez dice:
  octubre 3, 2016 a las 12:21 pm
  Buenas Jesús, me alegro de que te guste. En las próximas semanas veremos el mismo ejemplo mediante el método de recuperación estática y el de reducción de velocidad, que para mi es el óptimo, y permite diseñar una red más lógica y optimizada no solo desde el punto de vista del consumo energético, sino también desde el punto de vista del ahorro de material en los conductos.
  Accede para responder
rover dice:
octubre 7, 2016 a las 6:05 pm
Añadir solo un dato que puede ser de interés para algunos, dado que la presión estática disponible en los equipos se expresa en Pascales, hay que recordar que 1 mmca = 9,806 Pa.

Un saludo, Roverman.

P.S. ¿No se puede recuperar la contraseña en caso de olvido? Me registre de nuevo.
Accede para responder
- Fran Enríquez dice:
  octubre 8, 2016 a las 12:42 pm
  Hola Roverman, gracias por tu aportación. Efectivamente, es interesante tener presente esa conversión a la hora de elegir en catálogos de fabricantes. Algunos, como Soler & Palau, proporcionan sus curvas características tanto en mm.c.a como en Pa, pero es cierto que es interesante tener siempre clara dicha conversión.
  
  En cuanto a la recuperación de contraseña, es cierto que wordpress no da esa opción. Ya se lo he comentado a mi hermano, que lleva el tema de informática, para qe le de una solución y ponga un sistema de login más sencillo. En cualquier caso, si deseas recuperar tu anterior cuenta, puedo ponerte manualmente una contraseña fácil como «1234» y así puedes entrar de nuevo y poner la contraseña que desees.
  
  Gracias por tus comentarios.
  Un saludo compañero.
  
  Accede para responder
Cálculo de redes de distribución de aire (II) - CoolProyect dice:
octubre 9, 2016 a las 4:30 pm
[…] una semana más! Continuamos tratando el tema de las redes de distribución de aire, cuyo primer artículo publicamos la semana pasada. Hoy realizaremos el cálculo de la misma red mediante el método de […]
Accede para responder
Cálculo de redes de distribución de aire (III) - CoolProyect dice:
octubre 23, 2016 a las 12:58 pm
[…] haremos un breve estudio comparativo entre los tres métodos de cálculo, reducción de velocidad, pérdida de carga constante y recuperación estática, contrastando sus ventajas e inconvenientes en cuanto a coste de material […]
Accede para responder
CarlosMurillo dice:
enero 27, 2017 a las 7:53 pm
Es una informacion muy valiosa, mucho tiempo he buscado esto, felicitaciones, yo trabajo en el area de diseño en a/a y quiero agradecer por tomarse el tiempo a ayudar. veo que tienen una vision y tambien estoy dispispuesto a colaborar en cualquier cosa que este a mi alcance.
Accede para responder
- Fran Enríquez dice:
  enero 28, 2017 a las 1:43 pm
  Me alegro de que sea de tu interés el artículo Carlos. Bienvenido a nuestra web. Estamos buscando colaboradores y gente que quiera aportar sus conocimientos y hacer alguna entrada en el Blog. Ahora mismo está un poco parado, pero en un par de meses estará otra vez en marcha de nuevo.
  Si estás interesado en colaborar puedes enviarme un mensaje privado. Gracias!
  Un saludo.
  Accede para responder
Christian Camilo P Guancha dice:
enero 23, 2018 a las 11:35 pm
Buenas Tardes Para La extracción de vapor flash a 110 C° mediante campanas rectangulares, se utilizaría el mismo concepto como si fuese aire, pero se multiplica por un factor que interviene la densidad a esa temperatura? si tienes algun ejemplo te lo recomiendo

gracias

Accede para responder
acholaky dice:
abril 17, 2020 a las 12:14 am
Estimado Fran,
Me gustó. Bien clara la presentación.
Toda tu presentación está referida a ductos de fibra de vidrio.
Es factible que me indiques la fórmula de pérdida de carga para ductos de chapa galvanizada?. Es posible indicar las fuentes de la información?
Gracias y saludos.
acholaky
Accede para responder
Fran Enríquez dice:
abril 18, 2020 a las 10:40 am
Hola acholaky, las fórmulas de cálculo para conductos de fibra las he obtenido del Manual de climaver. Para conductos de chapa no he encontrado formula empírica, pero puedes emplear la fórmula de Darcy Weisbach y calcular el factor de fricción con el diagrama de Moody. Yo lo he hecho así algunas veces. No obstante los resultados no van a ser muy distintos a los calculados como si fuera conducto de fibra.
Accede para responder
Ariel dice:
mayo 17, 2020 a las 6:38 am
Buenas tardes, al parecer hay un error en la seleccion de la rejilla ya que el ducto es mas pequeño, favor confirmar, gracias
Accede para responder
Fran Enríquez dice:
mayo 17, 2020 a las 11:48 am
Hola Ariel, efectivamente la rejilla es de dimensiones superiores a las del conducto. Esto es bastante habitual, ya que las velocidades en el conducto son mayores y luego se debe disminuir la velocidad del aire a su paso por la rejilla para evitar corrientes de aire molestas y ruidos desagradables. La conexión de la rejilla con el conducto se soluciona con el conocido como «emboquillado». Para pasar de una sección a otra.
Un saludo.

Accede para responder
Ariel dice:
mayo 17, 2020 a las 6:29 pm
Gracias por su respuesta. Podría explicar como se realiza el equilibrado de una forma practica. gracias
Accede para responder
Fran Enríquez dice:
mayo 17, 2020 a las 7:09 pm
Hola, el equilibrado se puede hacer empleando un anemómetro, y en base a esa velocidad, conocida la sección útil de la rejilla, podemos saber el caudal de cada rejilla y cerrar la compuerta más o menos hasta obtener el caudal deseado. También podemos usar un medidor de caudal digital, que en base a la caída de presión entre la entrada y la salida de la rejilla puede estimar el caudal en m3/h gracias a la ley $\thinspace$ $Q=K\sqrt{P}$
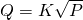
Un saludo.

Accede para responder
Ariel dice:
mayo 18, 2020 a las 12:52 am
Gracias por su ayuda
Accede para responder
FMatheu dice:
agosto 4, 2020 a las 9:38 pm
Hola. Gracias por el ejemplo!
Tengo una duda. Suponiendo que el tramo D-E tuviera 5 rejillas, se debe contemplar la pérdida de carga de la última rejilla o la sumatoria de las 5?
Gracias de antemano!
Saludos,

Accede para responder
Fran Enríquez dice:
agosto 11, 2020 a las 10:22 am
Hola FMatheu, solo habría que tener en cuenta la pérdida de carga de la rejilla más lejana, en este caso la última rejilla. Ya que si el ventilador es capaz de llegar con el caudal y presión a la última, también podrá llegar a las anteriores.
Un saludo.
Accede para responder
FMatheu dice:
febrero 18, 2021 a las 4:13 pm
Muchas gracias por su respuesta!
Al tratarse de un sistema de extracción o retorno, en los tramos donde se unan los caudales, ya no existe recuperación de presión sino es una pérdida adicional, correcto?
Accede para responder