¡Hola una semana más! Continuamos tratando el tema de las redes de distribución de aire, cuyo primer artículo publicamos la semana pasada. Hoy realizaremos el cálculo de la misma red mediante el método de recuperación estática. Este método permite una optimización de la red desde el punto de vista del equilibrado de las pérdidas de carga y disminuye el consumo energético, aunque la superficie de conductos es mayor que en otros métodos. Se recomienda haber leído previamente el artículo Redes de distribución de aire (I), ya que esta segunda parte se basa en comentarios realizados en esa entrada.

Cálculo de redes de distribución de aire (I)
octubre 2, 2016
Cálculo de redes de distribución de aire (III)
octubre 23, 2016CÁLCULO DE CONDUCTOS POR EL MÉTODO DE RECUPERACIÓN ESTÁTICA
Este método consiste en diseñar la red de conductos de tal forma que la pérdida de carga en cada tramo sea compensada por la recuperación estática obtenida en el tramo anterior. Así pues, el ventilador solo tendrá que proporcionar la presión necesaria para alcanzar la primera derivación. Es un método complejo de llevar a cabo manualmente, ya que requiere cálculo iterativo. No obstante, es sencillo de implantar mediante software. El objetivo de este artículo es conocer como funcionan los programas informáticos que emplean este método para desvelar lo que hay detrás de la «caja negra». Veámoslo aplicado al la red que nos ocupa. Recopilamos brevemente la información relevante del ejemplo del artículo anterior:
Diámetro equivalente:
(1) ![]()
Siendo:
![]() la altura del conducto
la altura del conducto
![]() la anchura del conducto
la anchura del conducto
Pérdidas de carga unitarias (mm.c.a/m) (Figura 1):
(2) ![]()
Siendo:
![]() el caudal de aire (m3/s)
el caudal de aire (m3/s)
![]() el diámetro equivalente (m)
el diámetro equivalente (m)
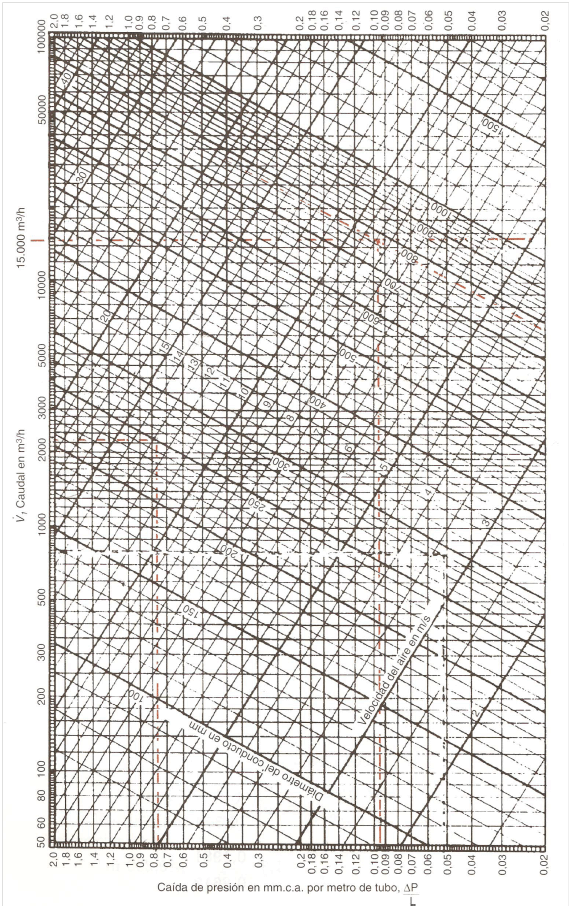
Figura 1. Gráfico para el cálculo de la pérdida de carga en conductos de fibra de vidrio.
Longitud equivalente (m): ![]() Longitud modificada del conducto, que incluye también las singularidades (codos, curvas y accesorios). Suele tomarse habitualmente como la longitud de tramo recto de conducto mayorada en un 50 %, es decir,
Longitud modificada del conducto, que incluye también las singularidades (codos, curvas y accesorios). Suele tomarse habitualmente como la longitud de tramo recto de conducto mayorada en un 50 %, es decir, ![]()
Recuperación estática (mm.c.a):
(3) ![]()
Siendo:
![]() la velocidad antes de la descarga de aire (m/s)
la velocidad antes de la descarga de aire (m/s)
![]() la velocidad después de la descarga de aire (m/s)
la velocidad después de la descarga de aire (m/s)
Caudal vs Sección:
(4) ![]()
Siendo:
![]() el caudal volumétrico de aire (m3/s)
el caudal volumétrico de aire (m3/s)
![]() la velocidad del aire (m/s)
la velocidad del aire (m/s)
![]() la sección útil del conducto (m2)
la sección útil del conducto (m2)
CÁLCULO DE LA RED
En la Figura 2 podemos ver el esquema de la red.
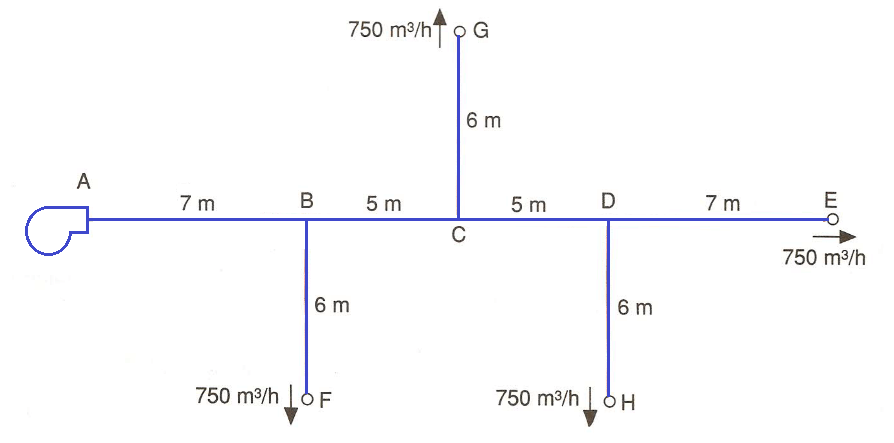
Figura 2. Esquema de la red de distribución de aire.
Longitudes y caudales de cada tramo (Tabla 1):
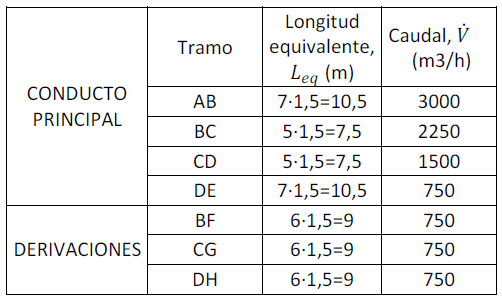
Tabla 1. Longitudes equivalentes y caudales de cada tramo.
CONDUCTO PRINCIPAL
– Tramo AB
Procedemos como hicimos en el método de pérdida de carga constante:
![]()
Conducto de 600×200 mm → SAB=0,12 m2 → vAB=6,94 m/s → DeqAB = 365 mm → hfAB = 0,2 mm.c.a/m
– Tramo BC
Se trata de compensar la pérdida de carga de este tramo con la recuperación estática que se genera tras la descarga de aire en el Punto B. Esto nos permite establecer la siguiente igualdad:
![]()
![]()
![]()
Sustituyendo los parámetros conocidos:
(5) ![]()
En esta ecuación tenemos dos incógnitas. Necesitamos ayudarnos de la ecuación de continuidad:
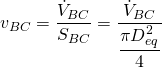
Sustituyendo los parámetros conocidos:
(6) ![]()
Resolviendo por iteraciones sucesivas el sistema formado por las Ecuaciones 5 y 6 obtenemos que DeqBC = 376 mm. Ahora debemos seleccionar un conducto rectangular aproximadamente equivalente de altura 200 mm, obteniendo el siguiente resultado:
- Conducto 650×200 mm
- DeqBC = 378 mm
- vBC = 4,81 m/s
- hfBC = 0,1 mm.c.a/m
Puesto que el conducto rectangular elegido tiene un Deq levemente mayor al obtenido en las ecuaciones de equilibrio, tendremos un pequeño exceso de presión estática respecto a la pérdida de carga:
![]()
![]()
![]()
Este exceso de presión, ΔHBC, se acumulará como presión disponible para el siguiente tramo. Si seleccionáramos el conducto con el diámetro exacto obtenido de las ecuaciones de equilibrio, no existiría tal exceso de presión, siendo la presión de recuperación estática justamente igual a las pérdidas del tramo, objetivo teórico del método de recuperación estática.
– Tramo CD
Procediendo como en el Tramo BC:
![]()
![]()
Obsérvese que a la ecuación de equilibrio, hemos añadido el exceso de presión estática acumulado en el Tramo BC, ![]() .
.
Sustituyendo los parámetros conocidos:
![]()
Añadimos la ecuación de continuidad:
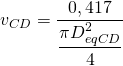
Resolviendo obtenemos que DeqCD = 344 mm. Ahora debemos seleccionar un conducto rectangular aproximadamente equivalente de altura 200 mm, obteniendo el siguiente resultado:
- Conducto 550×200 mm
- DeqCD = 352 mm
- vCD = 3,79 m/s
- hfCD = 0,068 mm.c.a/m
Puesto que el conducto rectangular elegido tiene un Deq levemente mayor al obtenido en las ecuaciones de equilibrio, tendremos un pequeño exceso de presión estática respecto a la pérdida de carga:
![]()
![]()
![]()
– Tramo DE
Ahora debemos añadir a la pérdida de carga del Tramo DE, la pérdida de carga de la rejilla al final del tramo. Seleccionaremos una rejilla del catálogo que tenga una baja pérdida de carga, ya que este método está orientado a conseguir bajas pérdidas de presión. Elegimos la rejilla de 525×225 mm, para 750 m3/h y una pérdida de carga de 0,625 mm.c.a:
![]()
![]()
Sustituyendo los parámetros conocidos:
![]()
Añadimos la ecuación de continuidad:
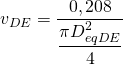
Resolviendo obtenemos que DeqDE = 361 mm. Ahora debemos seleccionar un conducto rectangular aproximadamente equivalente de altura 200 mm, obteniendo el siguiente resultado:
- Conducto 600×200 mm
- DeqDE = 365 mm
- vDE = 1,74 m/s
- hfDE = 0,016 mm.c.a/m
Vamos a ver ahora cuanta presión nos sobra tras cruzar la rejilla E, presión sobrante que debemos eliminar regulando la rejilla levemente:
![]()
![]()
![]()
Según esto, tenemos que regular la rejilla E para una pérdida de carga adicional de 0,064 mm.c.a.
Una vez calculados todos los tramos del conducto principal, recopilemos los datos obtenidos en la Tabla 2:
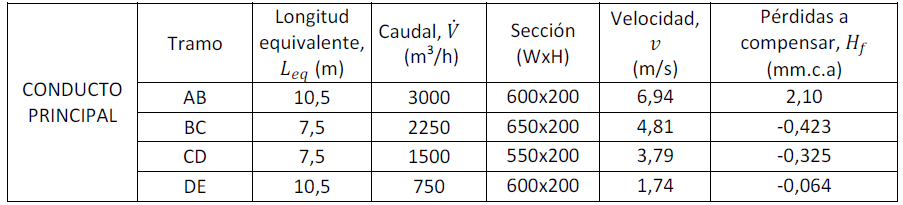
Tabla 2. Resultados de cálculo del conducto principal.
En la columna «Pérdidas a compensar» vemos que solo tenemos pérdidas de carga netas en el Tramo AB, mientras que en los siguientes tramos, la recuperación estática supera a las pérdidas de carga hasta llegar a la rejilla E al final de conducto principal, donde nos sobran 0,064 mm.c.a.
Por tanto, la presión en cabeza (Punto A), que será la necesaria a aportar por el ventilador, será HA = 2,10 mm.c.a, justo la necesaria para vencer las pérdidas del primer Tramo AB. El resto de tramos se cubren con la recuperación estática.
Así pues, el ventilador que seleccionemos deberá de proporcionar un caudal de 3000 m3/h y una presión de 2,10 mm.c.a.
Queda definido el conducto principal y el ventilador. Vamos ahora a calcular las derivaciones.
DERIVACIONES
Puesto que en todas las derivaciones el caudal es igual al de la boca de impulsión del Punto E (750 m3/h), seleccionaremos las mismas rejillas que en dicho punto. Esto es, rejillas de 525×225 mm, con pérdida de carga 0,625 mm.c.a.
El proceso de cálculo de las derivaciones es idéntico al empleado en el cálculo del último tramo del conducto principal (Tramo DE), teniendo en cuenta la presión estática acumulada antes de la derivación, y la pérdida de carga generada por la rejilla.
– Tramo BF
![]()
![]()
Sustituyendo los parámetros conocidos:
![]()
Añadimos la ecuación de continuidad:
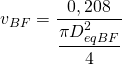
Resolviendo obtenemos que DeqBF = 254 mm. Ahora debemos seleccionar un conducto rectangular aproximadamente equivalente de altura 200 mm, obteniendo el siguiente resultado:
- Conducto 300×200 mm
- DeqBF = 266 mm
- vBF = 3,47 m/s
- hfBF = 0,075 mm.c.a/m
Presión sobrante tras cruzar la rejilla F:
![]()
![]()
![]()
Hay regular la rejilla F para una pérdida de carga adicional de 0,393 mm.c.a.
– Tramo CG
![]()
![]()
Sustituyendo los parámetros conocidos:
![]()
Añadimos la ecuación de continuidad:
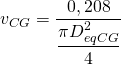
Resolviendo obtenemos que DeqCG = 292 mm. Ahora debemos seleccionar un conducto rectangular aproximadamente equivalente de altura 200 mm, obteniendo el siguiente resultado:
- Conducto 400×200 mm
- DeqCG = 305 mm
- vCG= 2,60 m/s
- hfCG = 0,039 mm.c.a/m
Presión sobrante tras cruzar la rejilla G:
![]()
![]()
![]()
Hay regular la rejilla G para una pérdida de carga adicional de 0,214 mm.c.a.
– Tramo DH
![]()
![]()
Sustituyendo los parámetros conocidos:
![]()
Añadimos la ecuación de continuidad:
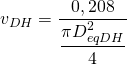
Resolviendo obtenemos que DeqDH = 355 mm. Ahora debemos seleccionar un conducto rectangular aproximadamente equivalente de altura 200 mm, obteniendo el siguiente resultado:
- Conducto 600×200 mm
- DeqDH = 365 mm
- vDH= 1,74 m/s
- hfDH = 0,016 mm.c.a/m
Presión sobrante tras cruzar la rejilla H:
![]()
![]()
![]()
Hay regular la rejilla H para una pérdida de carga adicional de 0,214 mm.c.a.
Ya podemos recopilar toda la información del cálculo de la red en una tabla resumen:
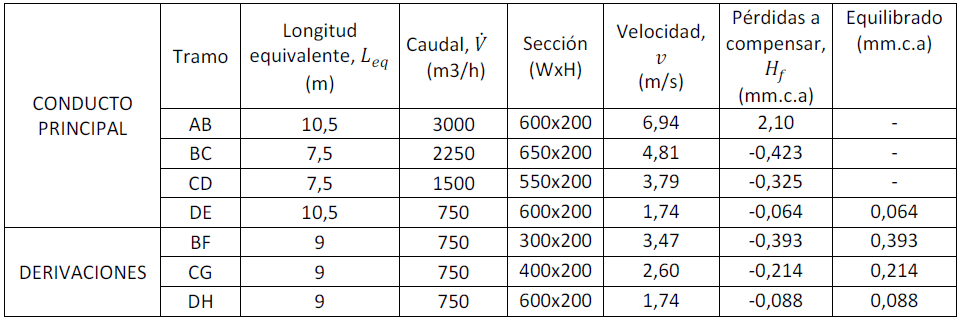
Tabla 3. Resumen del cálculo de la red por el método de recuperación estática.
Y aquí termina este artículo. Como podemos ver, en comparación con el método de pérdida de carga constante, tenemos velocidades más bajas en la red y por tanto menor pérdida de carga, pero a costa de mayores dimensiones en los conductos, que además son poco intuitivas en cuanto a la sucesión de diámetros. Por otra parte, este es el método más complicado de llevar a cabo de manera manual. La semana que viene continuaremos con el método de reducción de velocidad, el cual es, en mi opinión, el más intuitivo y práctico para llevar a cabo manualmente de manera rápida. ¡Buen domingo!
¿Te gustó este artículo? ¡Compártelo!




16 Comments
[…] compañeros, pues hasta aquí llega esta entrada. La semana que viene continuaremos con el método de recuperación estática. Espero que os sea de interés. Si hay cualquier duda, por favor, escribid en comentarios y estaré […]
[…] entre los tres métodos de cálculo, reducción de velocidad, pérdida de carga constante y recuperación estática, contrastando sus ventajas e inconvenientes en cuanto a coste de material e instalación, y costes […]
Estimado, me podía por favor explicar de mejor manera como es que consigue el resultado del diametro equivalente en el tramo BC, no consigo resolverla y obtener el resultado que a tu obtuviste, por favor, lo necesito para mi proyecto de titulación…
Hola Macarena. Para hallar el diámetro del tramo BC hay que realizar iteraciones sucesivas mediante las ecuaciones 5 y 6, ya que las incógnitas están implícitas. Consiste en dar un valor a v en la ecuación 6 y despejar D, luego sustituir D en la ecuación 5 y despejar v, si el valor de v hallado no coincide con el que hemos supuesto, hay que volver a empezar. Con una hoja excel se hace muy rápido el tanteo.
Un saludo.
Muchas gracias por responder, pero igual quede en duda, la verdad es que yo y mi profesor habiamos pensado en iterar los valores del Diámetro Equivalente, no el de la velocidad, pero siento que no estoy obteniendo valores correctos.
Y como serian los valores que le debo dar a la Velocidad?, desde 1 al límite (7.4m/s) ???
Estimado, ya entendí y lo comprobé con excel, pero tengo otra duda, como es que se obtuvo una seccion de 200×600???
al reemplazar en la ecuación de DiametroEquivalente, reemplace la altura por 200, y el diametro por 376, y obtengo un ancho de 641.043, no los 650…
porque sucede eso?
Gracias por todo, es para mi proyecto de titulo, de ingeniería informática, y estoy desarrollando un software que calcula una red de conducto en un plano, utilizando el método de recuperación estática, por lo que tengo que estar bien segura de las ecuaciones, ya que los monogramas no me sirven mucho a la hora de programar.
Hola Macarena, es simplemente un redondeo, ya que habitualmente los saltos en las medidas de los conductos se suelen normalizar de 50 en 50 mm, por lo que redondeamos a 650 mm, lo que hace que el conducto sea más fácil de fabricar y llevar a la práctica del montaje.
Me parece muy interesante el software que estás desarrollando. Estamos en Coolproyect elaborando software y nos interesaría tener informáticos que quisieran colaborar con nosotros. Puedes ver lo que estamos desarrollando aquí. Si te parece bien podríamos hablar y comentar tu proyecto y la posibilidad de desarrollar software con nosotros en Coolproyect. Te interesa? Puedes enviarme un email a fjenriquez@coolproyect.es o escribirme al 653036444.
Un saludo.
Amigo, muchas gracias por responder, aún no puedo responder a tu ofrecimiento, ya que aún tengo problemas con mi proyecto de titulo, mi tiempo esta 100% en ello, y otros problemas más :(.. colapsada.
Y ahora tengo otra duda, todo tu artículo del método de recuperación estática está muy bien explicado, y todo funciona correctamente cuando realizo ejemplos con caudales altos, como los tuyos, pero a la hora de usar caudales bajos, como es el caso del caudal necesario en viviendas para 2 personas (vivienda normal, clase media), todo se va al carajo, los diámetros son muy pequeños, el ancho y alto igual, la velocidad bajar enormemente.. y no se si eso está bien, no hay mucha información en Internet respecto a ésto, lo único que encuentro son listas de diámetros, pero el mínimo es de 200mm, lo cuál resulta muy grande para lo que necesito….
Amigo me podrías echar una manito con esto por favor, voy a desesperarme si no encuentro una buena respuesta…
Muchas gracias, desde ya por todo tu tiempo.
Saludos.
Ante todo gracias por este aporte que has hecho. Personalmente estoy tratanto de aprender todo este cacao.
Verás, estoy siguiendo el ejemplo que has puesto y creo que hay una errata. Corrígeme si me equivoco.
En el tramo BC, dices que hay que reiterar hasta que el valor de Vbc, se aproxime al inicial. Pues bien, la reiteración final se consigue cuandoel valor Vbc es aproximádamente 5.63 m/s con lo que se obtiene un diametro equivalente de 0.376 m, lo que equivale a una sección de 650×200, y para esta sección el diametro equivalente es 0.384 con una nueva velocidad de 5.39 m/s y no el valor de 4.86 que has puesto. ¿Correcto?
Hola,
Amigo, se calcula ahora la velocidad con la nueva sección.
secciónBC = 0.65×0.20 = 0.13
vBC= caudalBC/secciónBC, vBC=0.625/0.13 = 4.81
Espero haberte ayudado, saludos.
Hola Torm3nta, bienvenido/a a nuestro portal. Efectivamente, como indica Macarena, para calcular la velocidad real hay que hacerlo con la sección real 650×200 mm y no con el Diámetro equivalente. El Diámetro equivalente solo es una modelización para estimar la pérdida de carga, pero no es equivalente a la sección rectangular respecto a la velocidad. Es decir, el Diámetro equivalente es el del conducto circular equivalente que tiene la misma pérdida de carga que el conducto rectangular asociado, pero no la misma velocidad, puesto que las secciones son distintas.
Un cordial saludo.
Saludos y gracias a ambos por vuestra ayuda.
Entonces si me he enterado bien, resulta que de las sucesivas iteraciones, se obtiene una velocidad, y para un conducto circular, de aproximádamente 5.63 m/s que corresponde con un diámetro equivalente de una sección circular de 0.376 m. De esto se obtiene que la sección rectangular que necesitamos es de 650×200 mm, y que la velocidad para dicha sección rectangular, es de 4.8 m/s. ¿Correcto?
Por otro lado, al calcular la pérdida de carga unitaria, el caudal a introducir está en función de la sección cuadrada y de su respectiva velocidad, dividido por el diámetro equivalente de la sección cuadrada obtenida, que en este caso es de 0.378. ¿Correcto?
Se me plantea también la duda de que al hablar de sección 650×200, ¿estamos hablando de dimensiones del interior del conducto? Porque entiendo que los conductos tienen un cierto espesor de chapa ¿o bien los espesores de chapa no afectan apreciablemente al cálculo de las velocidades?
Saludos de nuevo. Me voy aclarando poco a poco gracias a esta guia y con el tiempo que dispongo.
Me surje la duda de cómo obtienes que para el tramo DE, se usa una rejilla de 525×225 y que la pérdida de carga para dicha rejilla es de 0.625 mm.c.a, para un caudal de 750 m3/h. ¿Entiendo que no has interpolado?
Porque si digamos, interpolamos entre caudales de 600 y 800 m3/h, tenemos que x1=600, y1=17 Pa, x2=800, y2=29 Pa, interpolando para un caudal de 750 m3/h, tenemos que (y-17)/(29-17) = (750-600)/(800-600)->y=26 Pa = 2.6 mmc.a
¿En qué estoy metiendo la pata?
Hola amigo.
Dice «Seleccionaremos una rejilla del catálogo que tenga una baja pérdida de carga, ya que este método está orientado a conseguir bajas pérdidas de presión.»
Las rejillas de 600 y 800 que tienen baja pérdida de carga son las siguientes.. ver imgaen–> (https://drive.google.com/file/d/1bu-v_ZLZV6G8oOHID7bHXSEhLjCnlq4c/view?usp=sharing)
Ahora al interpolar obtendrás una perdida de carga de 0.625 mm.c.a.
Espero te sirva mi respuesta, saludos.
Hola Torm3nta, la interpolación se realizaría de la siguiente forma:
(1)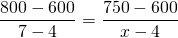
(2)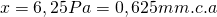
En cuanto a las dimensiones de los conductos, estas son interiores.
Un saludo!
Buenas Tardes,
Me gustaria saber si existe algun estandar para calcular las perdidas de carga que genera una rejilla dada. No somos capaces de tener una refrigeración correcta del equipo y una de las hipotesis que tenemos es el reducido caudal de aire por el radiador debido a las elevadas perdidas de carga tanto en las rejillas de admisión como descarga.
Un Saludo
iu